creatyde-Asemic
Spheres and Sets
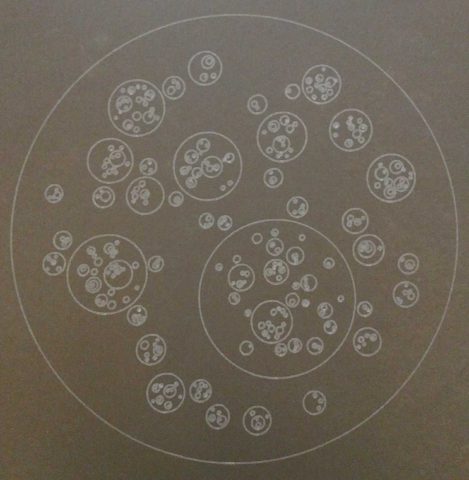
The notion of conceptually pleasing societies of spheres is fascinating to me. What would it be like? To have such a complex structure, a society, be made of such simple objects, a sphere? To a human, the observer of this society, what would characterize their interactions with each other as being both meaningful and dynamic?
Asemic language and writing has allowed me to consider one of the most fundamental questions of a group of socially interacting beings. How do they communicate as they interact? Communication, and thus the language it rests on, is about transferring meaningful information.
So, imagine that in this society of spheres, communication is not so much from individual to individual. It is from the society, all of the spheres as a collective, to itself. The society will create an arrangement of spheres: spheres containing one another like shells over shells. An arrangement is complex enough that it can carry an idea, like a symbol carries a concept. Each sphere within the society can examine the overall arrangement and change their relationship to other spheres. Then, the overall arrangement will change, symbolizing an idea closer to what each sphere may find more appealing at the moment.
Any idea in the sphere society can be represented by some unique structure (of spheres within spheres). Whenever multiple instances of the same structure appear, they represent the same idea. Every structure except the empty structure (a sphere not containing anything), contains other structure, and thus the idea the original structure represents contains other ideas. A structure can contain multiple copies of another structure, but it essentially just carries the idea represented by the structures (so duplication of structures within a structure is irrelevant to the meaning of the larger structure).
In this way, spheres cooperate with each other to create their language. To us humans, we may be baffled by the meaning of different structures we see in their language. To the spheres, however, the language allows them to relate themselves to each other and change the structure of their society. Their language allows them to see ideas on a microscopic scale as well as a macroscopic, from local ideas (within them or around them) to the idea embodied by all of society (should it rest within a gigantic sphere and form a unified structure).
The asemic writing piece shown at the very top is a snapshot of how the spheres might look like at one time, from a two-dimensional perspective.
Reflection
I wanted to incorporate aspects of set theory into my language because I am interested in set theory’s potential in abstracting our world and the logic that we know works within it. I originally planned to make a set theory representation of the human language and render a poem using a 3D directed graph with edges (containment) between the different nodes (sets). However, I was greatly concerned about the appearance of the final output and decided to rethink how set theory could be applied to a language. I was already interested in the simplicity of spheres, and so was appealed by the thought that if they could interact, they would interact in a way that naturally incorporated set theory.
In terms of technique, it was difficult to get a visually perfect piece. The code below generates a random configuration of circles using some rules to maximize aesthetics. It took many tries to adjust the parameters and regenerate the image. I chose a darker paper and lighter drawing material to give the feeling of chalk on a blackboard, as if humans were studying the curious beings. If I could have used actual chalk that would not dull, it is likely the piece would have look closer to what I wanted. I was also trying to make sure that the circles were relatively spaced out and varying in size and arrangement.
GIF of AxiDraw

Code
import processing.pdf.*; //__________________________________________________________________________ // canvas dimensions public static int widthCanvas = 1000; public static int heightCanvas = 1000; // circles must be within 0.9 of radius of parent circle public static float within = 0.9; // minimum radius of a circle public static float radLimit = 2; public static float radPerLimit = 0.03; // limits on radius as a percentage of min distance of circle center // to peer circle centers /** public static float lowerRadAm = 0.4; public static float upperRadAm = 0.8; **/ public static float meanRad = 0.6; public static float stdRad = 0.1; //__________________________________________________________________________ public class Circle { // position public float x; public float y; // radius public float radius; // dynamic array of circles within public ArrayList contains; } public class LineSegment { // length of line segment public float len; // angle of line in radians, 0 pointing right, going counterclockwise public float theta; } // checks if xp, yp are within circle defined by public boolean checkBoundary(float xp, float yp, Circle c) { float xDist = c.x - xp; float yDist = c.y - yp; float effRad = c.radius * within; if (xDist * xDist + yDist * yDist <= effRad * effRad) return true; return false; } // find line (mag, angle) between (x1,y1) and (x2,y2) from first point public LineSegment findLine(float x1,float y1, float x2,float y2) { float xDist = x2 - x1; float yDist = y2 - y1; float len = sqrt(xDist * xDist + yDist * yDist); float theta = atan2(yDist, xDist); LineSegment line = new LineSegment(); line.len = len; line.theta = theta; return line; } public Circle makeCircle(float xPos, float yPos, float rad) { // make circle Circle c = new Circle(); c.x = xPos; c.y = yPos; c.radius = rad; c.contains = new ArrayList(); // draw circle, do by diameter, not radius ellipse(xPos, yPos, rad*2, rad*2); // # of attempts based on size of circle int attempts = (int) (log(rad)*sqrt(rad)); //log(rad)*10 //random(log(rad)*5, log(rad)*10); float xp, yp, r; float maxRad, currDist; LineSegment line; Circle peer, currCirc; boolean reject; // do attempts to make circle inside for (int i = 0; i < attempts; i++) { // define position (within square) xp = random(xPos-rad*within, xPos+rad*within); yp = random(yPos-rad*within, yPos+rad*within); // check if position properly within parent circle if (!checkBoundary(xp, yp, c)) continue; // assuming point now inside circle, // find line between parent proper-border and point line = findLine(xPos,yPos, xp,yp); maxRad = (rad*within - line.len); // determine if should reject, based on positioning to peers // also keep track of minimum distance between point and peers reject = false; for (int j = 0; j < c.contains.size(); j++) { // get another circle within parent peer = c.contains.get(j); line = findLine(xp,yp, peer.x,peer.y); currDist = line.len - peer.radius; if (currDist < 0) { reject = true; break; } if (currDist < maxRad) maxRad = currDist; } if (reject) continue; // make radius of current circle r = maxRad * max(0,min(1,(randomGaussian() * stdRad + meanRad))); if (r < radLimit || r < radPerLimit * rad) continue; // make circle currCirc = makeCircle(xp, yp, r); // add circle to list of contains c.contains.add(currCirc); } return c; } //__________________________________________________________________________ void setup() { // size(widthCanvas,heightCanvas); size(1000, 1000, PDF, "circles.pdf"); noLoop(); // only draw once stroke(0); strokeWeight(1); noFill(); } void draw() { background(255); // make first circle, of specific dimensions Circle root = makeCircle(widthCanvas/2, heightCanvas/2, widthCanvas/2*within); exit(); } //__________________________________________________________________________ |