I am currently taking a mechanical engineering course called Stress Analysis. The course focuses on how forces on structures cause internal stresses, deflections, and failure. Part of the course involves creating a structure that meets the following criteria:
- Structural members are composed of only aluminum
- The structure lifts a 1lb weight at least 2 in. vertically. The weight is free to slide vertically on a rod.
- The structure, including the lift mechanism (in this case a servo motor), weight less than 1.25 lbs
- The structure is fixed at four points on a rigid playing field. A wall with a hole forces the structure to navigate a strange geometry to reach the weight.
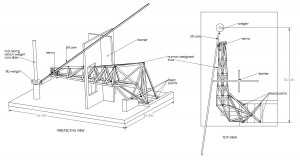
this is a truss I designed in solid works just using intuition and the constraints of the problem. I am hoping a GA could find a much stranger, lighter solution.
In addition the goals are to optimize for minimum weight or maximum lift. My plan is to make a computer program that performs a type of optimization search to generate a truss which minimizes weight and deflection (bending). Trusses are idealized structures composed of straight members connected at points. Trusses are entirely made of triangles, and each joint allows all of its members to rotate freely. This creates a condition where all of the members are in pure tension or pure compression. This is much simpeler to model computationally, and it creates very rigid structures.
The type of optimization search I plan on using (for now; there are many heuristics and some, like simulated annealing, may be better for this problem) is a type of Genetic Algorithm (GA) that uses a mixture of continuous and discrete variables. The vertices of the truss have x,y,z dimensions that are continuos variables. The edges are discrete (the are indices from the vertex matrix that choose which vertices to connect). This leads to a pretty complex problem, especially if there can be any number of vertices and edges. Conventional optimization methods, like steepest descent, which rely on analytic or calculus-based methods cannot work for this sort of problem because the parameters are related to each other and to the fitness (also called the cost) in extremely complex ways.
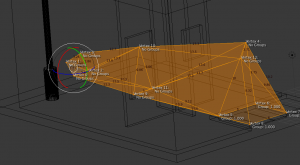
this is the template truss that gets imported as an obj into matlab (the program you are seeing this in is blender)
So far I this is what I have built (in matlab)
- import an obj, convert to truss gene structure
- populate a matrix with random trusses based on this template truss
- assign cost and rank to each individual in the population (fitness is a combination of mass and calculated deflections. The deflection solver comes from here, thanks to one Hossein Rahami)
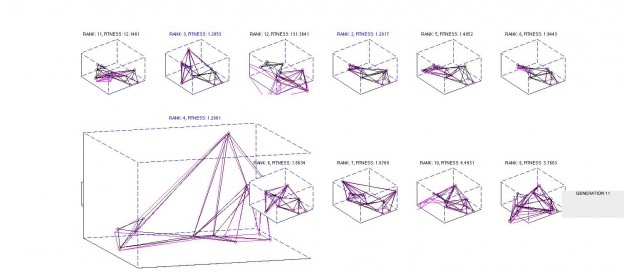
- visualize that generation (this needs serious work. right now it spits out a new window for each generation)
- assign mate pairs (highest ranked individuals)
- mate those pairs
- mutate the children with a mutation rate of around 20% of the total number of vertices
- repeat c until either maximum iterations is met or the difference between the best individual from the last generation and the best individual of the current generation is very small.
the details of each step, especially mutations and mating, make this either a brilliant powerful design tool that would likely converge on strange and beautiful solutions, or a nice way to fry the brain rapidly.
Currently the mating implements single-point crossover: a certain point along the genome is chosen at random and the genes from the opposite parent are spliced in. A better alternative might be splicing in specific coordinates instead of the whole vertex (X,Y and Z) or doing some sort of hybrid (interpolation) between trusses/points.
Mutations are limited to moving vertices by a number generated from a standard deviation multiplied by a constant. Really mutations need to include changes in topology like inserting or deleting edges and vertices, not just geometry (changing lengths and angles). Of course this will make gene combination a bit more tricky.
It’s also been a gigantic pain trying to get Matlab to let me do nice realtime animation. I guess I should just collect data as the algorithm runs and run an animation afterwards. I am really interested in visualizing the changes in individuals as well as plotting information about the algorithm’s behavior. This could include the average and best cost at each generation, point when previous parents were trumped by offspring, etc. I think this would make it easier to see how to improve the algorithm. One difficulty is that any component of the algorithm could be as complex as I wish. It is hard to have a good intuition about what areas could be modified to give maximum performance increase (I guess this calls for meta-optimization! ah!).